亚洲男人天堂av,国产一区二区久久精品,国产精品一区二区久久精品,国产精品久久久久久一区二区三区,五月婷婷在线观看视频,亚洲狠狠色丁香婷婷综合

下面分享2009年至2017年精選的23道高考題。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~

本文主要針對高考數(shù)學(xué)90分左右的學(xué)生。 希望對您有所幫助。

4-4主要講什么？ 方程的三個表達(dá)式！ 第一題主要測試三個方程的相互轉(zhuǎn)化。 4-4中出現(xiàn)的方程之前已經(jīng)學(xué)過。 為什么又要學(xué)習(xí)它們呢？ 正是因?yàn)檫@兩類方程非常容易處理某些類型的問題，所以第二個問題將考驗(yàn)這些簡單的技能。 我把這些簡單的計算大致分為四種。 高考幾乎就靠這四類題（國卷）

問題類型1：直線的標(biāo)準(zhǔn)參數(shù)方程t主要用于使用left|計算兩點(diǎn)之間的距離 t_1-t_2 右|

適用：當(dāng)問題需要兩點(diǎn)之間的距離并說出標(biāo)準(zhǔn)直線的參數(shù)方程時，或者給定直線的固定點(diǎn)和傾斜角度時

標(biāo)準(zhǔn)直線參數(shù)方程：x=x_0+tcosalpha \y=y_0+tsinalpha (t為參數(shù)) ((x_0,y_0)為直線上的不動點(diǎn)P) 設(shè)A為t=t_a

t=t_b 點(diǎn)，則 left| AB右| =左| t_a-t_b右| ,左| 美聯(lián)社右| =左| t_a右|

高考的考試很少原點(diǎn)到直線的距離公式，但是模擬題卻很多。

方法：同時結(jié)合直線的參數(shù)方程和曲線的常方程，得到關(guān)于t的二次方程，求出t_1，t_2，公式組，或者利用吠陀定理

問題類型2：極徑的含義主要用于使用left|計算兩點(diǎn)之間的距離 rho_1-rho_2right|

適用：問題要求兩點(diǎn)之間的距離且兩點(diǎn)都在經(jīng)過原點(diǎn)的直線上（經(jīng)過原點(diǎn)的公共直線：y=kx,theta =varphi）

方法：利用兩個聯(lián)立方程的極坐標(biāo)表示，求rho_1、rho_2組公式，或者集合吠陀定理

問題類型 3：求兩條曲線的交點(diǎn)

如果普通曲線方程是二變量的二次方程，則聯(lián)立求解非常復(fù)雜，因此采用極坐標(biāo)方程聯(lián)立求解。

如果普通方程很簡單，只需將普通方程組合起來即可。

方法：獲取聯(lián)立曲線的極坐標(biāo)方程結(jié)果（注意：這里有很多字母，需要知道哪一個是變量）

題型4：參數(shù)方程的含義

適用：在題干中，描述曲線上的一個（移動的）點(diǎn)。 不管是什么問題，這一點(diǎn)首先用參數(shù)方程來表達(dá)。

方法：移動點(diǎn)用參數(shù)方程表示

新課標(biāo)4-4試題統(tǒng)計：

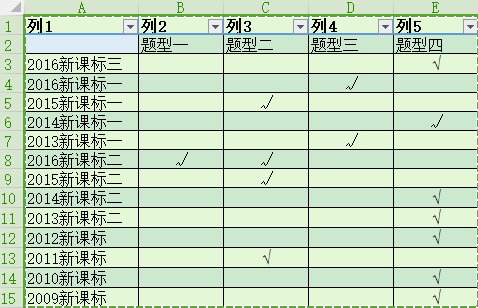
2017年全國第一：（題型4）

(1) 全部都可以轉(zhuǎn)化為普通方程并立即連接

(2)將C上的點(diǎn)用參數(shù)方程表示，然后采用點(diǎn)到直線距離公式。 難點(diǎn)在于計算。 sin(theta +varphi) 分別取 1 和 -1 得到兩個答案。

2017年國家二級：（題型2）

(1)方法仍然是通過代入求軌跡，只不過是設(shè)置在極坐標(biāo)中。 令 P(rho ,theta ), M(rho _1,theta ), |OP|=rho ,|OM|= rho _1=frac{4}{costheta }, 從 |OM |cdot |OP|=16原點(diǎn)到直線的距離公式，得到方程 C_2rho =4costheta (0">rho >0)

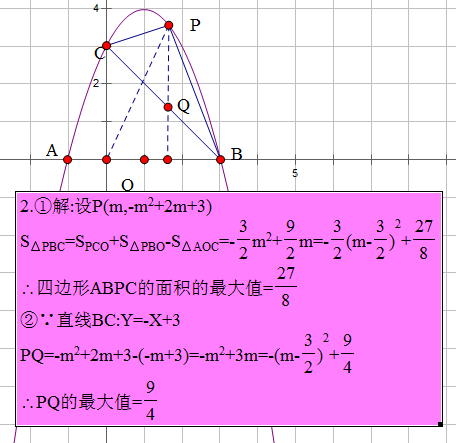
(2)S=frac{1}{2}|OA|cdot rho _{B}cdot sinangle AOB =4cosalpha cdot |sin(alpha -frac{ pi}{3})|簡化并找到最大值

2017年全國三級：()

(1)將方程同時解成普通方程，但字母較多，需要知道每個字母的含義

(2) 聯(lián)立L_3和C的極坐標(biāo)方程可求rho

這是我整理的2009年至2016年所有新課程標(biāo)準(zhǔn)中4-4題的精選題。

鏈接：/s/1sk8GvrJ 密碼：gm59