解析線性代數本質:向量、矩陣與線性變換的深度探索
更新時間:2024-06-10 21:17:01作者:佚名
什么是向量?
向量、基和線性相關的線性組合
矩陣和線性相關
矩陣乘法與線性變換相結合
三維空間中的線性變換
行列式
逆矩陣、列空間、秩和零空間
克萊默定律
非方陣
點積和對偶性
叉積
從線性變換的角度看叉積
基礎變換
特征向量和特征值
抽象向量空間
二階矩陣特征值的快速計算
張量、協方差、逆方差和秩
目錄
逆矩陣、列空間、秩和零空間
克萊默定律
逆矩陣、列空間、秩和零空間
之前我們通過直觀的線性變換理解了矩陣和向量的運算,也學習了線性變換如何描述對空間的操控。這對計算機圖形學和機器人學有很大的幫助,但線性代數的作用并不僅限于此。今天我們從另一個角度來看看線性代數如何幫助我們解決特殊的線性方程。

上面提到的特殊線性方程,所謂“特殊”是指未知量都是一階的,不包含其他特殊函數,如指數、對數、n 次方、三角函數等,且未知量乘以系數后相加。我們把這樣的方程組稱為:多元一階線性方程。
由于我們要用線性代數來解線性方程,所以我們需要將上述方程轉化為矩陣和向量乘法的形式。我們將系數提取成系數矩陣,將未知數提取成向量形式,將結果提取成向量形式,最后將它們轉化為:
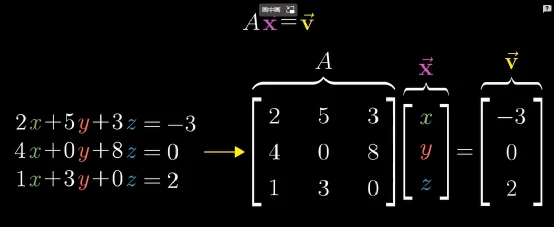
上面的矩陣乘法是不是看起來很熟悉?這就是前面提到的矩陣向量乘法。它的幾何意義是:向量
在矩陣A的作用下,矢量變換為
為了解決上述方程組,我們需要找到空間中的一個向量
對A和向量進行線性變換后
重合。

上面的例子是三維空間中的變換,為了更直觀的例子,我們來看二維空間中的例子:

那么我們如何判斷
有解決方案嗎?也就是說,是否存在一個向量
經過線性變換后,可以與矢量相結合
那重疊呢?這就要用到我們前面講過的行列式的知識了。在行列式章節中我們說過,矩陣行列式表示的是變換前后空間的縮放比例。根據行列式的不同,又可以分為行列式不為零和行列式為零兩種情況。
行列式不為零:
矩陣行列式不為零,說明經過線性變換后空間維數不變,即基向量沒有被壓縮成一條直線或者一個點,那么一定有一個向量
也就是說,我們一定能找到一個能與向量匹配的基向量縮放因子
重疊;如何找到
現在讓我們反過來想。我們剛剛找到了向量
在基質作用下,
巧合,反過來:變換矩陣A的逆矩陣
作用于載體
變換后的向量就是我們需要的向量。
這里我們直觀的看一下逆矩陣的含義,例如逆時針旋轉90度的變換如下:

相應的逆變換是順時針旋轉90度:

對任何向量應用變換,然后應用逆變換將使向量返回到其原始狀態,這意味著兩個矩陣的乘積是恒等變換。
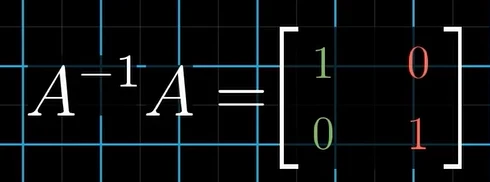
綜上所述,如果變換矩陣的行列式不為0,那么線性方程組有唯一解,這一點對于高維空間也適用。
行列式為零:
當變換矩陣的行列式為零時,即變換后基向量落在同一直線或點上。如果這條直線和向量
如果它們不共線,那么我們就找不到矢量
,這可以使x*i_transformed+y*j_transformed與向量v重合,也就是說,沒有逆變換可以將一條線解壓縮成一個面;但如果這條線與向量重合
共線,即使沒有逆變換,也可能有解,且解的個數是無窮大。

如上圖,棕紅色和綠色是變換后的基向量,黃色是結果向量
,同樣適用于三維空間。
注意,現在我們又想到了一個新名詞:秩。秩表示變換后空間的維數。前面舉的例子中,如果變換矩陣的行列式為0,說明空間被壓縮成了一條直線,因此空間維數為1,說明秩為1;如果變換矩陣的行列式不為零,說明空間沒有被壓縮,原空間是2維的,變換后的空間也是2維的,秩為2,原空間是3維的,變換后的空間也是3維的,秩為3;秩表示變換后空間的維數,不管變換結果是直線,平面還是三維空間,所有可能的變換結果的幾何體就稱為矩陣的列空間。

秩這個名字是怎么來的呢?如上圖所示,矩陣的列表示變換后基向量的位置。換句話說矩陣行列式的運算法則,列空間就是矩陣的列所占的空間,而秩就是列空間的維數。當秩達到最大值時,秩就等于列數。我們把這種情況稱為滿秩。
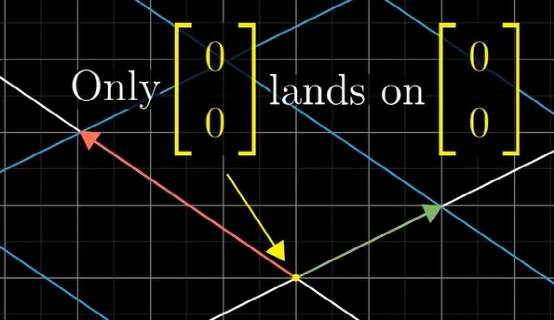
如下圖所示,線性變換必須保持原點的位置不變,原點就是零向量,當秩滿時,原點是變換后唯一落在原點的向量,當秩不滿時,由于空間被壓縮,部分序列的向量會被壓縮到原點。
克萊默定律
以前我們從線性代數的角度去理解線性方程,卻沒有給出具體的解法。今天我們來看一個計算規則以及背后的幾何原理:克萊姆規則。
首先我要聲明克萊姆法則并不是解線性方程最有效的方法,相比之下高斯消元法更快,學習克萊姆法則是為了拓展知識面,加深對線性方程的理解。
讓我們從一個簡單的例子開始。請注意,克萊默定律可以擴展到任意數量的未知數。

通過前面章節的學習,我們知道上述方程可以轉化為矩陣乘法的形式:

矩陣的前兩列表示變換后的基向量的坐標:
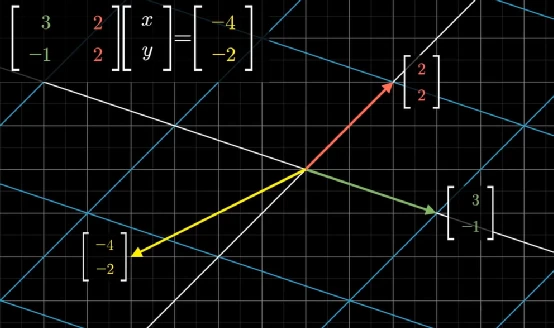
現在的問題是找出哪個向量將成為
。

一個想法是輸出矩陣
它是矩陣列向量的線性組合。現在我們需要做的就是找到x和y的值。

在上一章中我們說過,一個方程組是否有解取決于矩陣行列式的數值。如果行列式為0,則該方程無解或有無數個解。如果行列式不為0,則該方程組有唯一解。本文僅討論行列式不為0的情況。
在講克萊默定律之前,我們先來看一個錯誤的解法思路。我們知道一個向量可以分解為基向量的線性組合,如下圖所示。在變換之前,我們先計算未知向量
基礎向量上的分量。

并假設變換后上述向量分解定律仍然滿足:

理想很完美,但現實很殘酷。不幸的是,上面的公式可能不成立,因為變換后的基向量可能不垂直,或者可能會被拉伸。例如上圖中的紅色和綠色箭頭就是變換后的基向量。
是不是所有的變換都不滿足上面的公式呢?有一種特殊的變換,它變換后,基向量仍然垂直,長度不變。更一般地說,變換前垂直的向量在變換后仍然垂直。這種變換稱為正交變換。在計算機圖形學中,它對應于剛體運動,也就是說變換不會拉伸、壓縮或變形。
因此,如下圖所示,利用正交矩陣來解決線性關系問題非常方便:

改造前:

由于是正交變換,所以變換之后下面的公式依然成立矩陣行列式的運算法則,下面的公式中第一個是目標向量,第二個是變換之后基向量的位置,都是已知的。

最后結果:
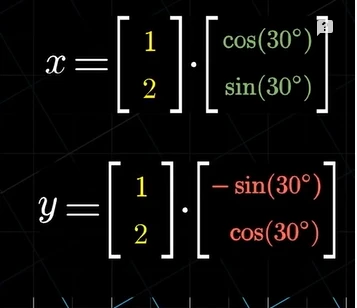
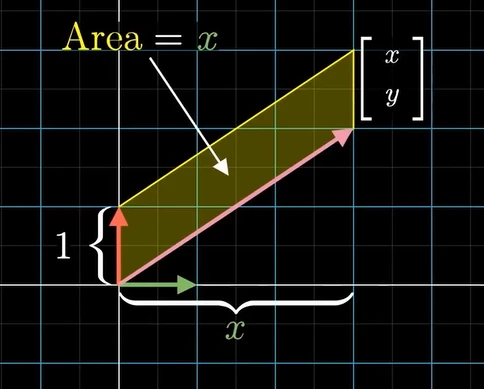
正交變換雖然是特例,但是卻給我們提供了一種思路,接下來進入今天的正題,如下圖所示,未知向量
和 i 形成的面積等于坐標 y。

類似地,未知向量
和j形成的面積等于坐標x。
類似地,在三維坐標系中,立方體的體積可以與 x、y 和 z 坐標相關聯。
為什么要把平行四邊形的面積和立方體的體積與坐標聯系起來呢?根據前面章節所學的知識,當對未知向量進行線性變換時,面積與體積的比值會發生變化。

轉型前
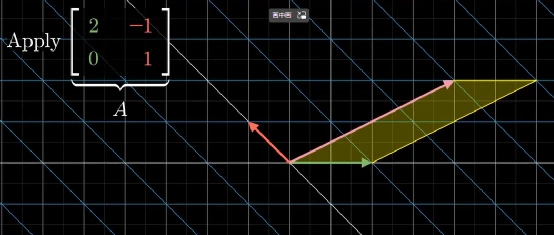
轉型后
根據我們在前面章節中學到的知識,當我們談論表面或體積的變換比率時,我們立即想到了行列式!面積擴展的比率等于變換矩陣的行列式。
變換前平行四邊形的面積等于y值英語作文網,變換后四邊形的面積按照變換矩陣的行列式進行縮放,其面積等于
。

轉型前

轉型后
然后我們可以利用變換后的面積和行列式的值來找到 y:

那么我們如何找到變換后的面積呢?我們已經知道變換后得到的向量的坐標
,那么它和i構成的四邊形的面積可以用矩陣計算
該矩陣的行列式表達式表示
變換矩陣,其行列式值表示變換前后面積變化的比率。

用同樣的方法我們可以找到另一個變量x的值:

對于三維來說也是如此:
